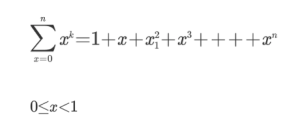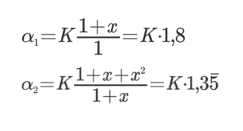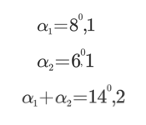Il logo Contec, nato dapprima per identificare la capostipite Contec Ingegneria e poi diventato logo di Gruppo, non è un semplice schema geometrico, ma è un grafico denso di contenuti culturali, formulati allo scopo di renderlo rappresentativo della complessità del gruppo.

Contec Ingegneria nasce nel 1962 come società che eroga servizi intellettuali atti a produrre opportunità in senso lato, applicando principi scientifici basati prevalentemente sulla matematica e sulla fisica ma anche sulla creatività, tutto fondato su solide basi culturali. L’apporto principale al processo creativo è stato fornito da collaboratori ingegneri ed architetti.

Il logo è stato creato in modo da rappresentare tali caratteristiche: è stato infatti concepito sulla base di complesse considerazioni utili ancora oggi per avere consapevolezza dell’origine della ricca e complessa realtà nella quale oggi ci riconosciamo e siamo riconosciuti.

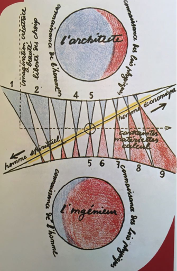
Fin dalle origini, Contec ha visto nella collaborazione tra ingegneri e architetti il fondamento della sua attività che comunque storicamente ha visto una prevalenza dei servizi di ingegneria. La bella immagine di Le Corbusier “L’architecte et l’ingénieur” era riprodotta e presente nella sede storica di Contec fin dall’inizio della sua storia.

La spiegazione

I solidi platonici o poliedri complessi regolari, studiati da Pitagora, da Platone e ripresi da Euclide, negli anni dal 400 al 300 a.c., dopo il Medioevo furono oggetto di interesse, nel Rinascimento, da parte di molti artisti.

In particolare Luca Pacioli, matematico, Leonardo Da Vinci e Piero della Francesca tra la fine del ‘400 e l’inizio del ‘500 studiarono nuovamente i poliedri e fornirono istruzioni per un loro corretto inserimento nelle opere d’arte, studiandone anche i cosiddetti schemi scheletrici.

 

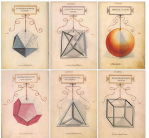
Ciò si vede dai bellissimi disegni di Leonardo inseriti nel trattato “De divina proporzione” di Luca Pacioli (sopra) e il trattato “De quinque corporibus regolaribus” di Piero del quale sotto é riportata una delle pagine sui tetraedri.

Proseguiamo arrivando a Verona dove, nella chiesa di Santa Maria in Organo, vi sono le bellissime tarsie di fra Giovanni degli anni 90 del ‘400. Una di queste è un trionfo di scheletri poliedrici, esibizione di capacità tecnica.

Da questi elementi nasce l’idea che, sia pure nella forma più semplice, lo scheletro di tetraedro può essere rappresentativo di capacità tecnica.

Ma Contec non è solo questo, la sua attività segue un percorso ideativo che parte da una prima immagine latente che, successivamente si consolida ed in conclusione si materializza in un oggetto di elevata qualità.
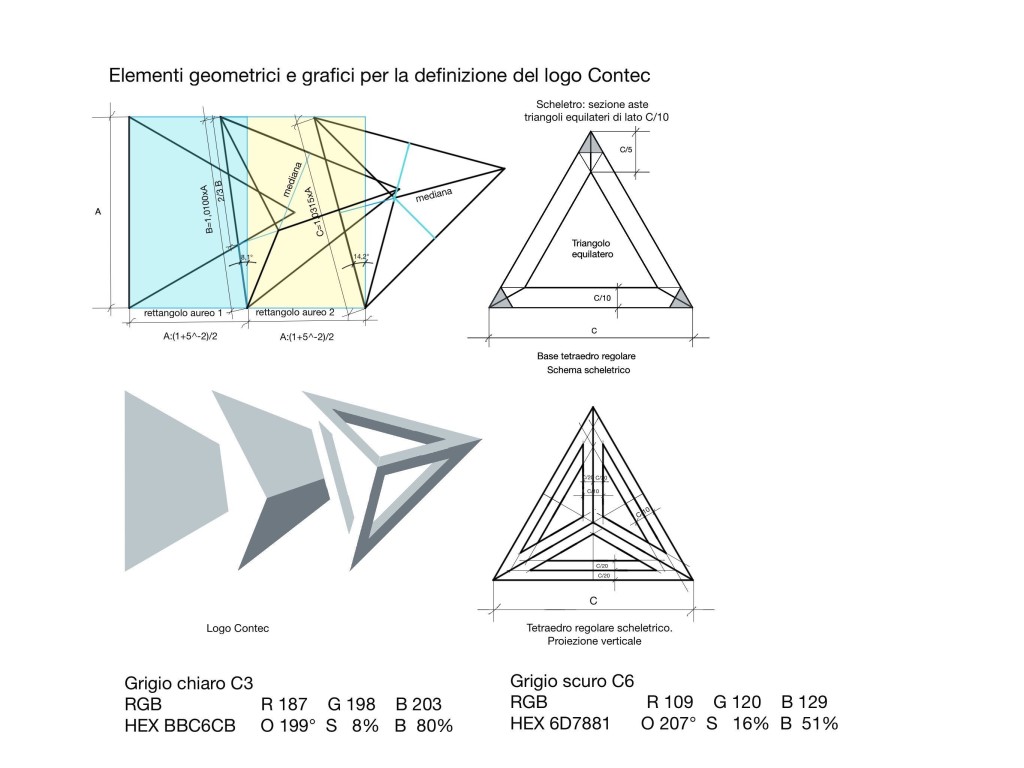
Ecco la spiegazione delle tre immagini in sequenza: un triangolo equilatero che si trasforma in tetraedro non regolare ma simmetrico e poi in un tetraedro regolare strutturato.

Come si vede dal logo in apertura di articolo, l’immagine nel contempo ruota in senso antiorario. É cioè presente un effetto dinamico. L’immagine si sviluppa nel tempo e avanza verso il risultato finale.
Le tre figure geometriche sono contenute in un reticolo ideale costituito da due rettangoli aurei in cui i nodi inferiori coincidono con i vertici inferiori dei triangoli.

La sezione aurea, chiamata dagli antichi anche costante di Fidia, scultore e architetto ateniese del IV secolo a.c., ribattezzata nel 1400 dal  matematico Luca Pacioli “divina proporzione” nota ai Babilonesi ed agli Egizi (piramide di Cheope), utilizzata come rettangolo aureo nella pianta del Partenone, è un numero irrazionale (1+5^-2)/2 usato in architettura.

I tre triangoli rotanti aumentano lievemente di dimensioni in modo progressivo per rispettare i confini del rettangolo aureo.

Come possiamo immaginare la velocità angolare? Le tre figure in sequenza ruotano secondo una regola matematica che riflettendo ho cercato di individuare.
Tutti ci ricordiamo della sfida tra Achille e la tartaruga. Fu proposta da Zenone di Elea nel’400 a.c. e poi ripresa da Aristotele. La regola matematica è tradotta nella serie geometrica convergente.

La serie si dice convergente perché la somma di infiniti termini converge su un numero finito.
E’ stato scelto per x il valore 0,8 che determina una convergenza sul numero 5. Siamo partiti da due rettangoli aurei (2), dal triangolo (3) siamo arrivati al tetraedro (4) per la convergenza all’infinito cinque (5). Ha una sua logica.
I due primi angoli di rotazione (tetraedro rispetto al triangolo e tetraedro strutturato rispetto al tetraedro) si ricavano dalle formule che seguono:

Il valore di K determina gli angoli reali. Per K è stato assunto il valore Π/40 con angoli in radianti, per esigenze grafiche (angoli piccoli). Risultano+ di conseguenza:

La riflessione da fare è la seguente: dalla prima traccia all’idea generale vi è un primo significativo passo (rotazione), dall’idea generale ai passi successivi le rotazioni (i cambiamenti e gli approfondimenti) proseguono con gradini sempre più piccoli fino a convergere nel risultato finale. Nel contempo le immagini si ingrandiscono (l’idea si consolida) e la figura si completa.

La storia non è ancora finita, abbiamo altri passaggi. Il logo contiene delle illusioni ottiche.

Noi vediamo delle linee che non ci sono. Non c’è bisogno di dire quali, ma per maggiore chiarezza possiamo evidenziare alcune immagini di scuola che sfruttano questa illusione.

Illusione dimostrata da Schumann nel 1904 e in modo più sistematico da Gaetano Kanizsa nel 1955. Pubblicato su “Illusione e realtà” edito da Scientifican American ed. 1977. L’illusione ottica inserita  ha lo scopo di segnalare la fantasia e l’immaginazione, che è bagaglio culturale essenziale di Contec.

Manca solo la scelta del colore: il grigio.

Il grigio è un colore neutro ma non solo. Il grigio è il colore che si ottiene mescolando in parti uguali i tre colori primari (blu, rosso e giallo). Può rappresentare l’ oggettività, l’equilibrio e la raffinatezza.
Nell’immaginario comune le persone sagge hanno grande esperienza da mettere a frutto, cioè possono utilizzare al meglio la materia grigia. Così Contec.

Articolo a cura di Maurizio Cossato, socio fondatore di Contec Ingegneria.